The example
Broadly speaking, a TLA+ proof is a collection of claims, arranged in a hierarchical structure which we describe below, where each claim has an assertion that is either unjustified or justified by a collection of cited facts. The purpose of TLAPS is to check the user-provided proofs of theorems, that is, to check that the hierarchy of claims indeed establishes the truth of the theorem if the claims were true, and then to check that the assertion of every justified claim indeed is implied by its cited facts. If a TLA+ theorem has a proof with no unjustified claims, then, as a result of checking the proof, TLAPS verifies the truth of the theorem.
We shall illustrate the TLAPS by proving the correctness of the Euclidean algorithm.
The algorithm
The well-known Euclidean algorithm can be written in the PlusCal language as follows:
The PlusCal translator translates this algorithm into a TLA+ specification that we could prove correct. However, in this tutorial, we shall write a somewhat simpler specification of Euclid's algorithm directly in TLA+.
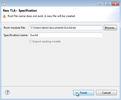
Creating a new TLA+ module
First of all, let us create a new specification within the ToolBox (click on the thumbnails to expand the screenshots).
Importing modules
In order to get the definitions of arithmetic operators
(
Definitions
We shall then define the GCD of two integers. For that purpose,
let us define the predicate "p divides q" as follows:
p divides q iff there exists some integer d in the interval 1..q
such that q is equal to p times d.
We then define the set of divisors of an integer q as the sets of integers which both belong to the interval 1..q and divide q:
We define the maximum of a set S as one of the elements of this set which is greater than or equal to all the other elements:
And finally, we define the GCD of two integers p and q to be the maximum of the intersection of Divisors(p) and Divisors(q):
For convenience, we shall also define the set of all positive integers as:
When we save the specification (with the menu File > Save), the toolbox launches the SANY syntactic analyzer and reports any errors that might appear.
Constants and variables
We then define the two constants and two variables needed to describe the Euclidean algorithm, where M and N are the values whose GCD is to be computed:
The specification
We define the initial state of the Euclidean algorithm as follows:
In the Euclidean algorithm, two actions can be performed:
- set the value of y to y - x if x < y
- set the value of x to x - y if x > y.
These actions are again written as a definition called
The specification of the algorithm asserts that the variables
have the correct initial values and, in each execution step, either
a
(For reasons that are irrelevant to this algorithm, TLA specifications always allow stuttering steps that leave all the variables unchanged.)
We want to prove that the algorithm always satisfies the following property:
Hence we want to prove the following theorem
named