A simple proof
The invariant
Intuitively, the theorem
That is,
Checking proofs
First we need to assume that constants
Let us then prove that
To check wether TLAPS can prove that theorem by itself, we declare its proof obvious.
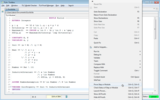
We can now ask TLAPS to prove that theorem, by
right-clicking on the line of the theorem (or use
the ctrl+G,ctrl+G / cmd-G,cmd-G shortcut), as shown in
the following screenshot:
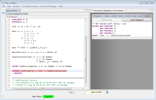
But TLAPS does not know how to prove the proof obligation corresponding to that proof. As you can see in the following screenshot, it prints that obligation and reports failures of three backends, Zenon, Isabelle, and SMT. The default behavior of TLAPS is to send obligations first to an SMT solver (by default Z3), then if that fails to the automatic prover Zenon, then if Zenon fails to Isabelle (with the tactic "auto"). See the tactics section to learn more about this process.
Using facts and definitions
As you can see, the obligation cannot be proved
because TLAPS treats the symbols
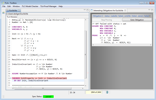
Unfortunately, the theorem is still colored red, meaning that
none of the back-ends could prove that obligation. As with
definitions, we have to specify which facts
are usable. In this case, we have to make the
fact
The general form of a
BY e1, …, em DEF d1, …, dn
which claims that the assertion follows by assuming e1, …, em and expanding the definitions d1, …, dn. It is the job of TLAPS to then check this claim, and also to check that the cited facts e1, …, em are indeed true.
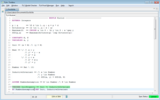
Finally, SMT succeeds in proving that obligation and the theorem gets colored green: